Fit examples, utilities, tips and tricks¶
A wide range of applications of the kafe core and the usage of
the helper functions is exemplified below. All of them
are contained in the sub-directory examples/ of the
kafe distribution and are intended to serve as a basis for
user projects.
Example 1 - model comparison¶
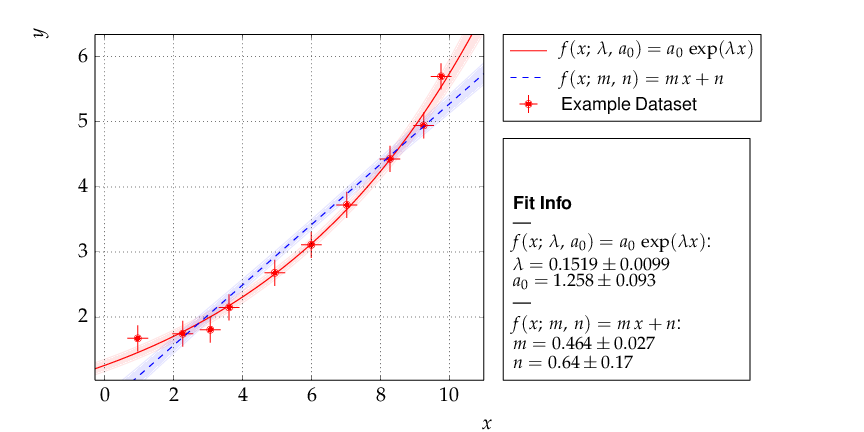
To decide whether a model is adequate to describe a given set of data, typically several models have to be fit to the same data. Here is the code for a comparison of a data set to two models, namely a linear and an exponential function:
# import everything we need from kafe
from kafe import *
# additionally, import the two model functions we want to fit:
from kafe.function_library import linear_2par, exp_2par
############
# Load the Dataset from the file
my_dataset = Dataset(input_file='dataset.dat', title="Example Dataset")
### Create the Fits
my_fits = [Fit(my_dataset, exp_2par),
Fit(my_dataset, linear_2par)]
### Do the Fits
for fit in my_fits:
fit.do_fit()
### Create the plots, save and show output
my_plot = Plot(my_fits[0], my_fits[1])
my_plot.plot_all(show_data_for=0) # show data only once (it's the same data)
my_plot.save('plot.pdf')
my_plot.show()
The file dataset.dat contains x and y data in the standard kafe data format, where values and errors (and optionally also correlation coefficients) are given for each axis separately. # indicates a comment line, which is ignored when reading the data:
# axis 0: x
# datapoints uncor. err.
0.957426 3.0e-01
2.262212 3.0e-01
3.061167 3.0e-01
3.607280 3.0e-01
4.933100 3.0e-01
5.992332 3.0e-01
7.021234 3.0e-01
8.272489 3.0e-01
9.250817 3.0e-01
9.757758 3.0e-01
# axis 1: y
# datapoints uncor. err.
1.672481 2.0e-01
1.743410 2.0e-01
1.805217 2.0e-01
2.147802 2.0e-01
2.679615 2.0e-01
3.110055 2.0e-01
3.723173 2.0e-01
4.430122 2.0e-01
4.944116 2.0e-01
5.698063 2.0e-01
The resulting output is shown below. As can be seen already from the graph, the exponential model better describes the data. The χ² probability in the printed output shows, however, that the linear model would be marginally acceptable as well:
linear_2par
chi2prob 0.052
HYPTEST accepted (CL 5%)
exp_2par
chi2prob 0.96
HYPTEST accepted (CL 5%)
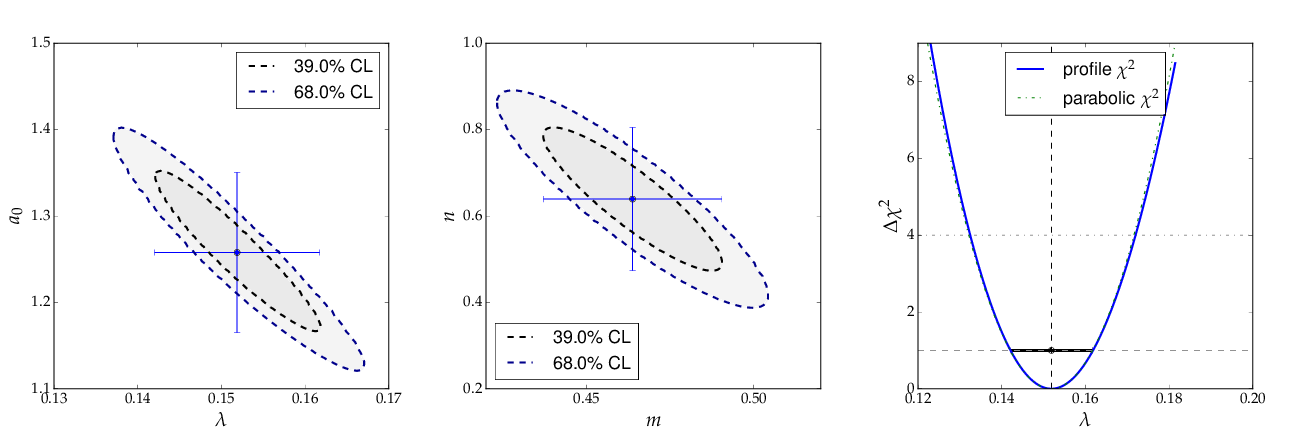
The contour curves of the two fits are shown below and reflect the large correlations between the fit parameters. The right plot of the profile χ² curve shows that there is a slight deviation from the parabolic curve in the fist fit of a non-linear (exponential) function. For more details on the profiled χ² curve see the discussion of example 3, where the difference is more prominent.
Example 2 - two fits and models¶
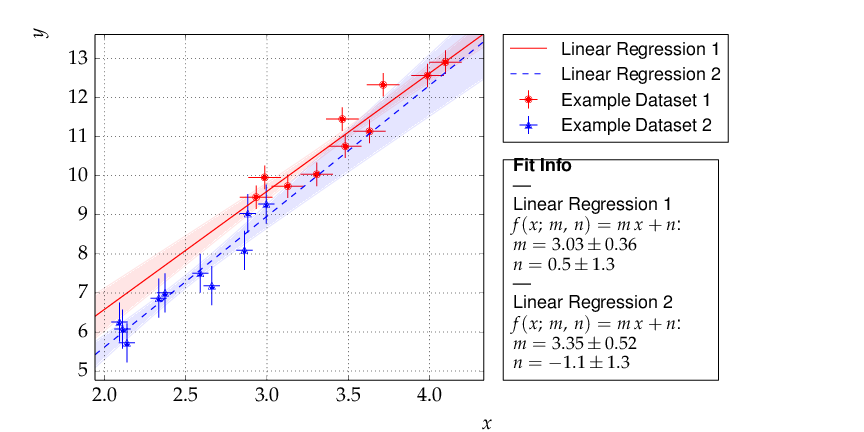
Another typical use case consists of comparing two sets of measurements and the models derived from them. This is very similar to the previous example with minor modifications:
...
############
# Workflow #
############
# Load two Datasets from files
my_datasets = [Dataset(input_file='dataset1.dat', title="Example Dataset 1"),
Dataset(input_file='dataset2.dat', title="Example Dataset 2")]
# Create the Fits
...
# Do the Fits
...
# Create the plots
my_plot.plot_all() # this time without any arguments, i.e. show everything
...
This results in the following output:
Although the parameters extracted from the two data sets agree within errors, the uncertainty bands of the two functions do not overlap in the region where the data of Dataset 2 are located, so the data are most probably incompatible with the assumption of an underlying single linear model.
Example 3 - non-linear fit with non-parabolic errors¶
Very often, when the fit model is a non-linear function of the parameters, the χ² function is not parabolic around the minimum. A very common example of such a case is an exponential function prarametrised as shown in the code fragment below. Minuit contains a spacial algorithm, Minos, which returns correct errors also in this case. Instead of using the curvature the minimum, Minos follows the χ² function from the minimum to the point where it crosses the the value minimum+up, where up=1 corresponds to one standard deviation in χ² fits. During the scan of the χ² function at different values of each parameter the minimum with respect to all other parameters in the fit is determined, thus making sure that all correlations among the parameters are taken into account. In case of a parabolic χ² function, the Minos errors are identical to those obtained by the Hesse algorithm, but are typically larger or asymmetric in other cases.
The method kafe.do_fit() executes the Minos algorithm
after completion of a fit and prints the Minos errors if
the deviation from the parabolic result are larger than 5% .
A graphical visualisation is provided
by the method plot_profile() , which
displays the profile χ² curve for the parameter
with name or index passed as an argument to the method.
The relevant code fragments and the usage of
the method kafe.fit.plot_profile() are
illustrated here:
...
# definition of the fit function
@ASCII(x_name="t", expression="A0*exp(-t/tau)")
# Set some LaTeX-related parameters for this function
@LaTeX(name='A', x_name="t",
parameter_names=('A_0', '\\tau{}'),
expression="A_0\\,\\exp(\\frac{-t}{\\tau})")
@FitFunction
def exponential(t, A0=1, tau=1):
return A0 * exp(-t/tau)
...
# Load the data, perform fit and plot
my_dataset = Dataset(input_file='dataset.dat', title="Example Dataset")
my_fit = Fit(my_dataset, exponential)
my_fit.do_fit()
my_plot = Plot(my_fit)
my_plot.plot_all()
# --> display contours and profile
contour = my_fit.plot_contour(0, 1, dchi2=[1.,2.3])
profile1=my_fit.plot_profile(0)
profile2=my_fit.plot_profile(1)
# Show the plots
my_plot.show()
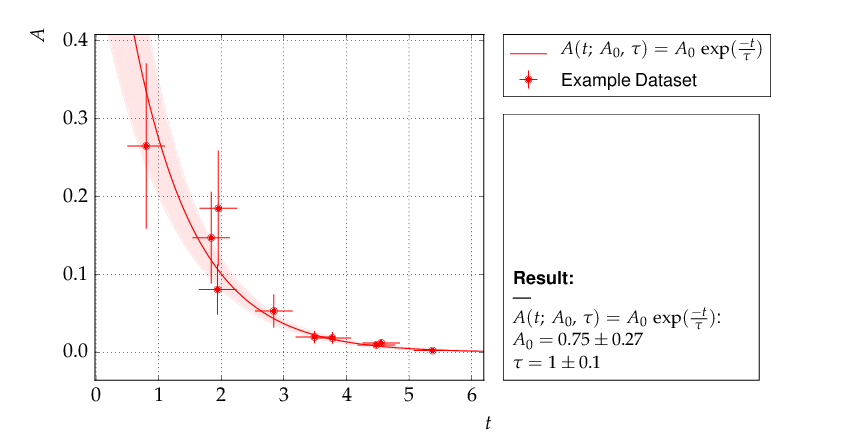
The data points were generated using a normalisation factor of A0=1. and a lifetime τ=1.. The resulting fit output below demonstrates that this is well reproduced within uncertainties:
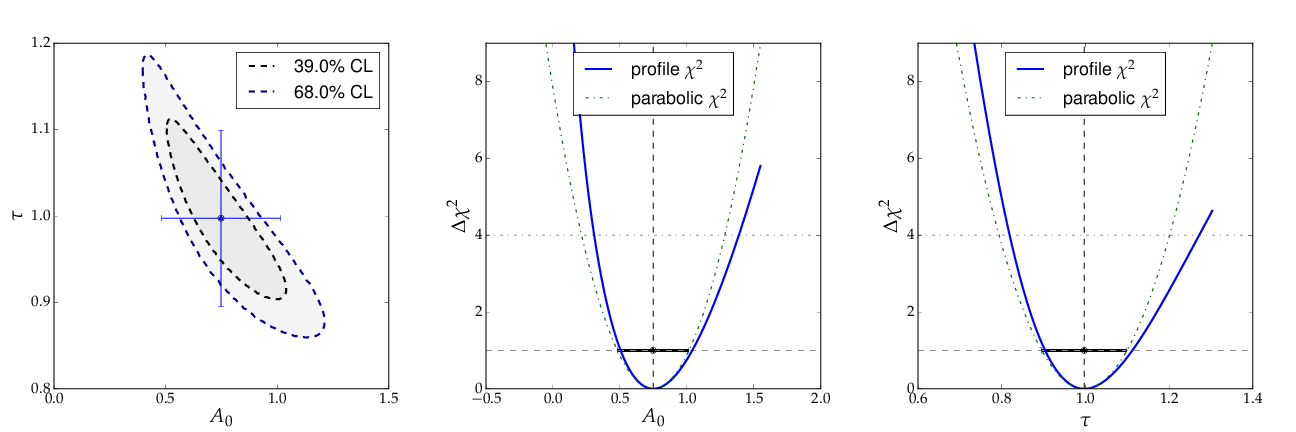
The contour A0 vs τ, however, is not an ellipse, as shown in the figure below. The profiled χ² curves are also shown; they deviate significantly from parabolas. The proper one-sigma uncertainty in the sense of a 68% confidence interval is read from these curves by determining the parameter values where the χ² curves cross the horizontal lines at a value of Δχ²=1 above the minimum. The two-sigma uncertainties correspond to the intersections with the horizontal line at Δχ²=4.
Note: a more parabolic behaviour is achieved by using the width parameter λ=1/τ in the parametrisation of the exponential function.
Example 5 - non-linear multi-parameter fit (damped oscillation)¶
This example shows the fitting of a more complicated model function
to data collected from a damped harmonic oscillator. In such
non-linear fits, stetting the initial values is sometimes crucial
to let the fit converge at the global minimum. The Fit
object provides the method set_parameters() for this
purpose. As the fit function for this problem is not a standard one, it is
defined explicitly making use of the decorator functions available in
kafe to provide nice type setting of the parameters. This time,
the function parse_column_data() is used to read
the input, which is given as separate columns with the fields
<time> <Amplitude> <error on time> <error on Amplitude>
Here is the example code:
...
from kafe import *
from numpy import exp, cos
# Model function definition #
# ===========================
# Set an ASCII expression for this function
@ASCII(x_name="t", expression="A0*exp(-t/tau)*cos(omega*t+phi)")
# Set some LaTeX-related parameters for this function
@LaTeX(name='A', x_name="t",
parameter_names=('a_0', '\\tau{}', '\\omega{}', '\\varphi{}'),
expression="a_0\\,\\exp(-\\frac{t}{\\tau})\,"
"\cos(\\omega{}\\,t+\\varphi{})")
@FitFunction
def damped_oscillator(t, a0=1, tau=1, omega=1, phi=0):
return a0 * exp(-t/tau) * cos(omega*t + phi)
# ---- Workflow #
# load the experimental data from a file
my_dataset = parse_column_data('damped_oscillation.dat',
field_order="x,y,xabserr,yabserr", title="Damped Oscillator",
axis_labels=['Time t', 'Amplitude'])
# --- Create the Fit
my_fit = Fit(my_dataset, damped_oscillator)
# Set the initial values for the fit:
# a_0 tau omega phi
my_fit.set_parameters((1., 2., 6.28, 0.8))
my_fit.do_fit()
# --- Create and output the plots
my_plot = Plot(my_fit)
my_plot.plot_all()
#my_plot.save('plot.pdf')
my_fit.plot_correlations() # all contours and profiles
my_plot.show()
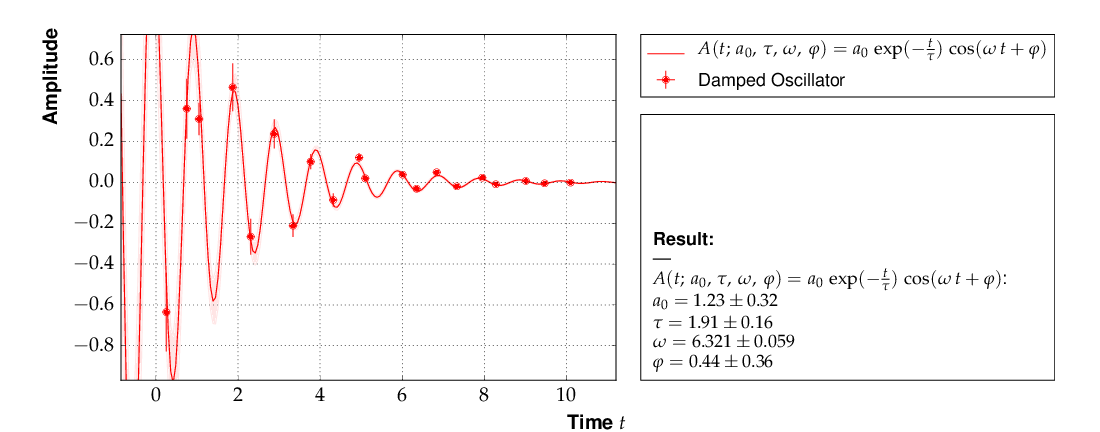
This is the resulting output:
The fit function is non-linear, and, furthermore, there ist not a single
local minimum - e.g. a shift in phase of 180° corresonds to a change in
sign of the amplitude, and valid solutions are also obtained for multiples
of the base frequency. Checking of the validity of the fit result is
threfore important. The method
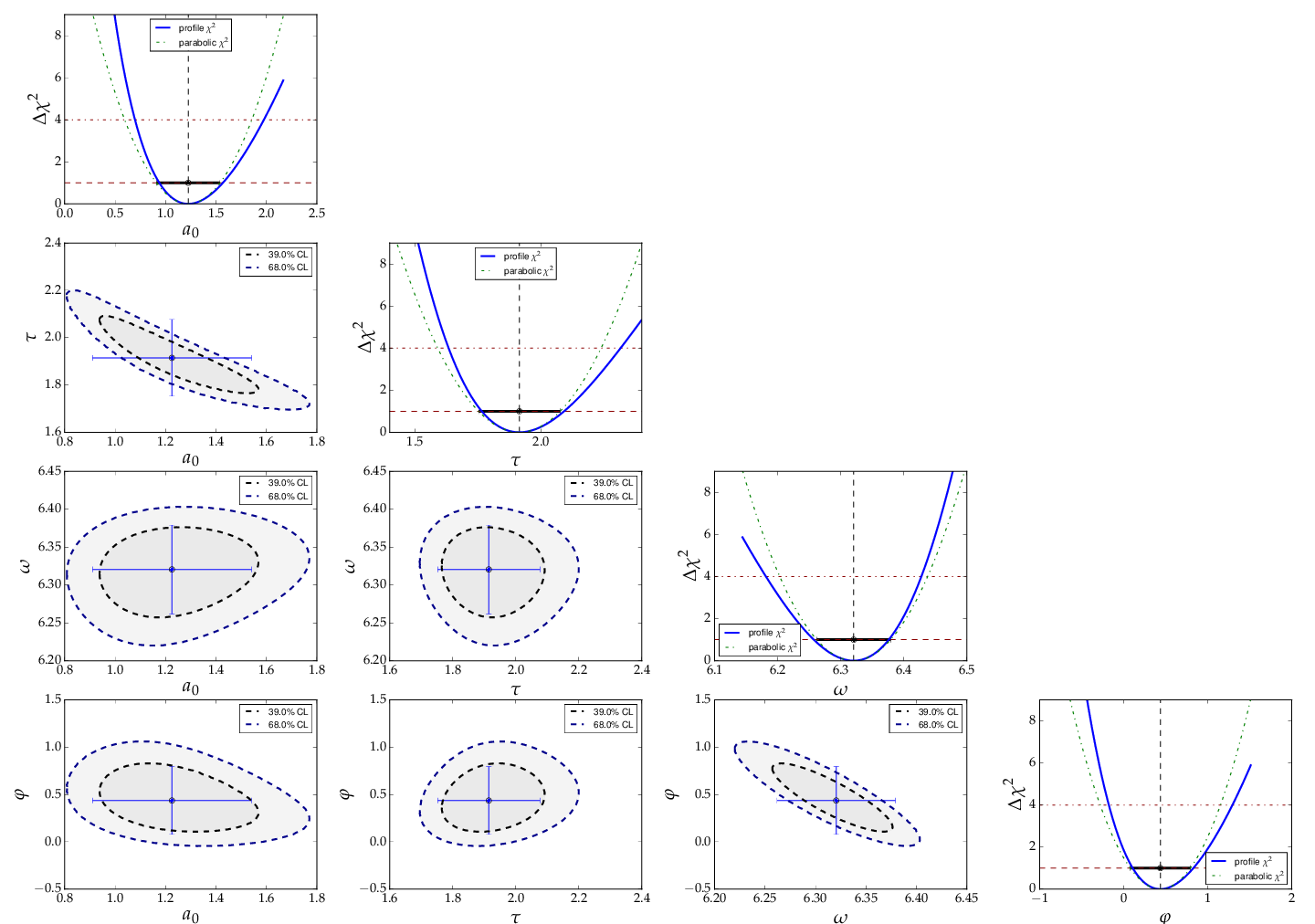
plot_correlations() provides the
contours of all pairs of parameters and the profiles for each of
the parameters and displays them in a matrix-like arrangement.
Distorted contour-ellipses show wether the result is affected
by near-by minima, and the profiles allow to correctly assign
the parameter uncertainties in cases where the parabolic
approximation is not precise enough.
Example 6 - linear multi-parameter fit¶
This example is not much different from the previous one, except that
the fit function, a standard fourth-degree polynomial from the module
function_library, is modified to reflect the names of the problem
given, and matplotlib functionality is used to influence the
output of the plot, e.g. axis names and linear or logarithmic scale.
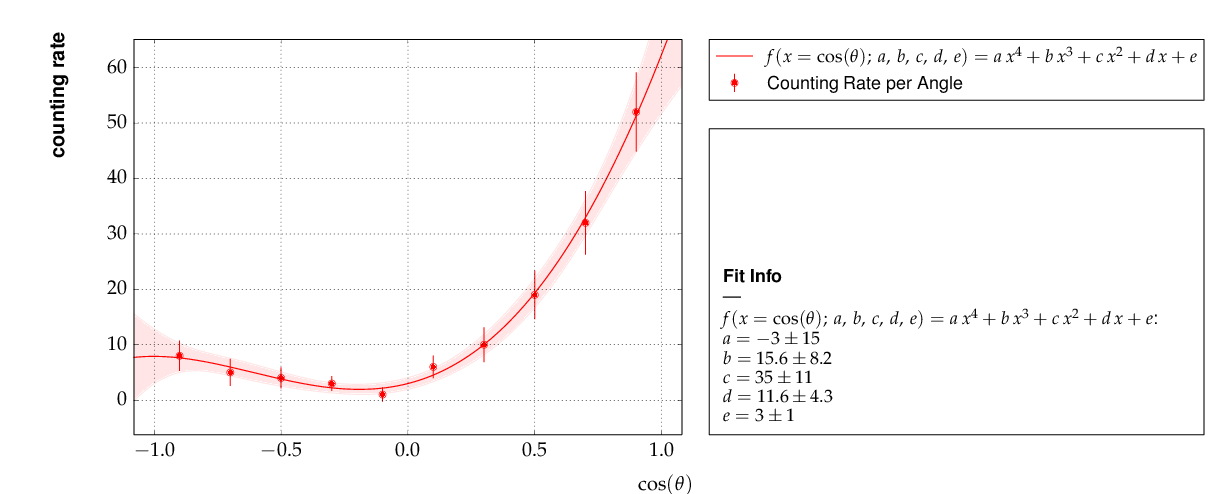
It is also shown how to circumvent a problem that often arises when errors depend on the measured values. For a counting rate, the (statistical) error is typically estimated as the square root of the (observed) number of entries in each bin. For large numbers of entries, this is not a problem, but for small numbers, the correlation between the observed number of entries and the error derived from it leads to a bias when fitting functions to the data. This problem can be avoided by iterating the fit procedure:
In a pre-fit, a first approximation of the model function is determined, which is then used to calculate the expected errors, and the original errors are replaced before performing the final fit. Note that the numbers of entries in the bins must be sufficiently large to justify a replacement of the (asymmetric) Poisson uncertainties by the symmetric uncertainties implied by the χ²-method.
The implementation of this procedure needs accesses some more fundamental methods of the Dataset, Fit and FitFunction classes. The code shown below demonstrates how this can be done with kafe, using some of its lower-level, internal interfaces:
from kafe.function_library import poly4
# modify function's independent variable name to reflect its nature:
poly4.x_name = 'x=cos(t)'
poly4.latex_x_name = 'x=\\cos(\\theta)'
...
# Set the axis labels appropriately
my_plot.axis_labels = ['$\\cos(\\theta)$', 'counting rate']
...
# load the experimental data from a file
my_dataset = parse_column_data(
'counting_rate.dat',
field_order="x,y,yabserr",
title="Counting Rate per Angle")
### pre-fit
# error for bins with zero contents is set to 1.
covmat = my_dataset.get_cov_mat('y')
for i in range(0, len(covmat)):
if covmat[i, i] == 0.:
covmat[i, i] = 1.
my_dataset.set_cov_mat('y', covmat) # write it back
# Create the Fit
my_fit = Fit(my_dataset, poly4)
# fit_label="Linear Regression " + dataset.data_label[-1])
# perform an initial fit with temporary errors (minimal output)
my_fit.call_minimizer(final_fit=False, verbose=False)
# set errors using model at pre-fit parameter values:
# sigma_i^2=cov[i, i]=n(x_i)
fdata = my_fit.fit_function.evaluate(my_fit.xdata,
my_fit.current_parameter_values)
np.fill_diagonal(covmat, fdata)
my_fit.current_cov_mat = covmat # write new covariance matrix
### end pre-fit - rest is as usual
my_fit.do_fit()
# Create the plots and ==
my_plot = Plot(my_fit)
# -- set the axis labels
my_plot.axis_labels = ['$\\cos(\\theta)$', 'counting rate']
# -- set scale linear / log
my_plot.axes.set_yscale('linear')
...
This is the resulting output:
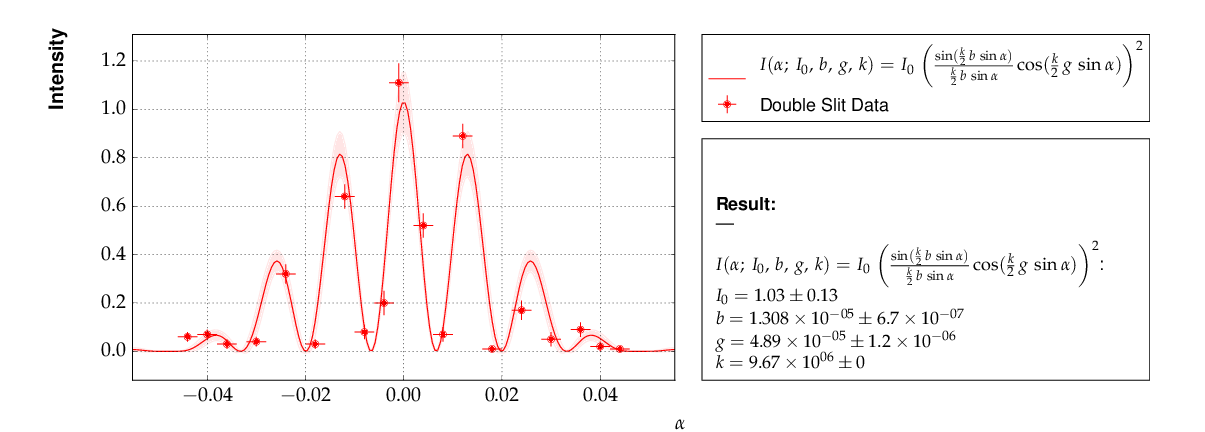
Example 7 - another non-linear multi-parameter fit (double-slit spectrum)¶
Again, not much new in this example, except that the model is now very non-linear, the intensity distribution of light after passing through a double-slit. The non-standard model definition again makes use of the decorator mechanism to provide nice output - the decorators (expressions beginning with ‘@’) can safely be omitted if LaTeX output is not needed. Setting of appropriate initial conditions is absolutely mandatory for this example, because there exist many local minima of the χ² function.
Another problem becomes obvious when carefully inspecting the fit function definition: only two of the three parameters g, b or k can be determined, and therefore one must be kept fixed, or an external constraint must be applied. Failing to do so will result in large, correlated errors on the parameters g, b and k as an indication of the problem.
Fixing parameters of a model function is achieved by the method
fix_parameters(), and a constraint within a given uncertainty
is achieved by the method constrain_parameters()
of the Fit class.
Here are the interesting pieces of code:
...
# Model function definition #
# Set an ASCII expression for this function
@ASCII(x_name="x", expression="I0*(sin(k/2*b*sin(x))/(k/2*b*sin(x))"
"*cos(k/2*g*sin(x)))^2")
# Set some LaTeX-related parameters for this function
@LaTeX(name='I', x_name="\\alpha{}",
parameter_names=('I_0', 'b', 'g', 'k'),
expression="I_0\\,\\left(\\frac{\\sin(\\frac{k}{2}\\,b\\,\\sin{\\alpha})}"
"{\\frac{k}{2}\\,b\\,\\sin{\\alpha}}"
"\\cos(\\frac{k}{2}\\,g\\,\\sin{\\alpha})\\right)^2")
@FitFunction
def double_slit(alpha, I0=1, b=10e-6, g=20e-6, k=1.e7):
k_half_sine_alpha = k/2*sin(alpha) # helper variable
k_b = k_half_sine_alpha * b
k_g = k_half_sine_alpha * g
return I0 * (sin(k_b)/(k_b) * cos(k_g))**2
...
# Set the initial values for the fit
# I b g k
my_fit.set_parameters((1., 20e-6, 50e-6, 9.67e6))
# fix one of the (redundant) parameters, here 'k'
my_fit.fix_parameters('k')
...
If the parameter k in the example above has a (known) uncertainty, is is more appropriate to constrain it within its uncertainty (which may be known from an independent measurement or from the specifications of the laser used in the experiment). To take into account a wave number k known with a precision of 10‘000 the last line in the example above should be replaced by:
...
my_fit.constrain_parameters(['k'], [9.67e6], [1.e4])
...
This is the resulting output:
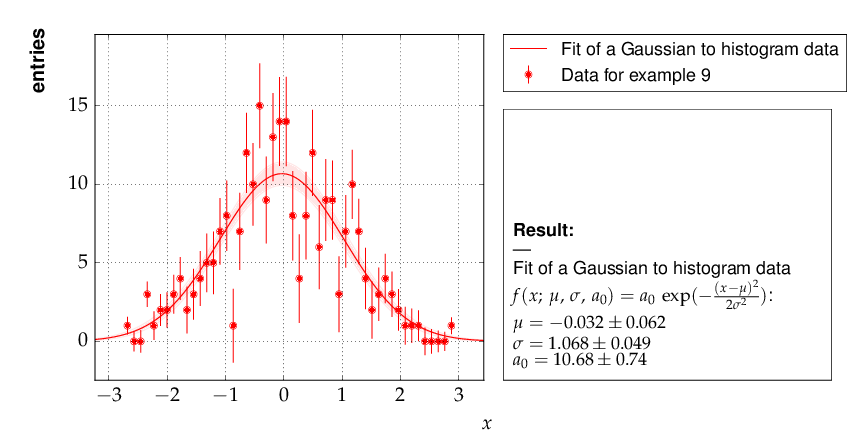
Example 9 - fit of a function to histogram data¶
This example brings us to the limit of what is currently
possible with kafe. Here, the data represent the
center of a histogram bins ad the number of entries, 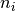 ,
in each bin. The (statistical) error is typically estimated
as the square root of the (observed) number of entries in each bin.
For large numbers of entries, this is not a problem,
but for small numbers, especially for bins with 0 entries,
the correlation between the observed number of entries and
the error derived from it leads to a bias when fitting
functions to the histogram data. In particular, bins with
zero entries cannot be handled in the χ²-function, and are
typically omitted to cure the problem. However, a bias
remains, as bins with downward fluctuations of the
observed numbers of events get assigned smaller errors
and hence larger weights in the fitting procedure - leading
to the aforementioned bias.
,
in each bin. The (statistical) error is typically estimated
as the square root of the (observed) number of entries in each bin.
For large numbers of entries, this is not a problem,
but for small numbers, especially for bins with 0 entries,
the correlation between the observed number of entries and
the error derived from it leads to a bias when fitting
functions to the histogram data. In particular, bins with
zero entries cannot be handled in the χ²-function, and are
typically omitted to cure the problem. However, a bias
remains, as bins with downward fluctuations of the
observed numbers of events get assigned smaller errors
and hence larger weights in the fitting procedure - leading
to the aforementioned bias.
These problems are avoided by using a likelihood method for such use cases, where the Poisson distribution of the uncertainties and their dependence on the values of the fit model is properly taken into account. However, the χ²-method can be saved to some extend if the fitting procedure is iterated. In a pre-fit, a first approximation of the model function is determined, where the error in bins with zero entries is set to one. The model function determined from the pre-fit is then used to calculate the expected errors for each bin, and the original errors are replaced before performing the final fit. Note that the numbers of entries in the bins must be sufficiently large to justify a replacement of the (asymmetric) Poisson uncertainties by the symmetric uncertainties implied by the χ²-method.
The code shown below demonstrates how to get a grip on such more complex procedures with more fundamental methods of the Dataset, Fit and FitFunction classes:
...
# Load Dataset from file
hdataset = Dataset(input_file='hdataset.dat', title="Data for example 9")
# error for bins with zero contents is set to 1.
covmat = hdataset.get_cov_mat('y')
for i in range(0, len(covmat)):
if covmat[i, i] == 0.:
covmat[i, i] = 1.
hdataset.set_cov_mat('y', covmat) # write it back
# Create the Fit instance
hfit = Fit(hdataset, gauss, fit_label="Fit of a Gaussian to histogram data")
#
# perform an initial fit with temporary errors (minimal output)
hfit.call_minimizer(final_fit=False, verbose=False)
#
#re-set errors using model at pre-fit parameter values:
# sigma_i^2=cov[i, i]=n(x_i)
fdata=hfit.fit_function.evaluate(hfit.xdata, hfit.current_parameter_values)
np.fill_diagonal(covmat, fdata)
hfit.current_cov_mat = covmat # write back new covariance matrix
#
# now do final fit with full output
hfit.do_fit()
# and create, draw, save and show plot
...
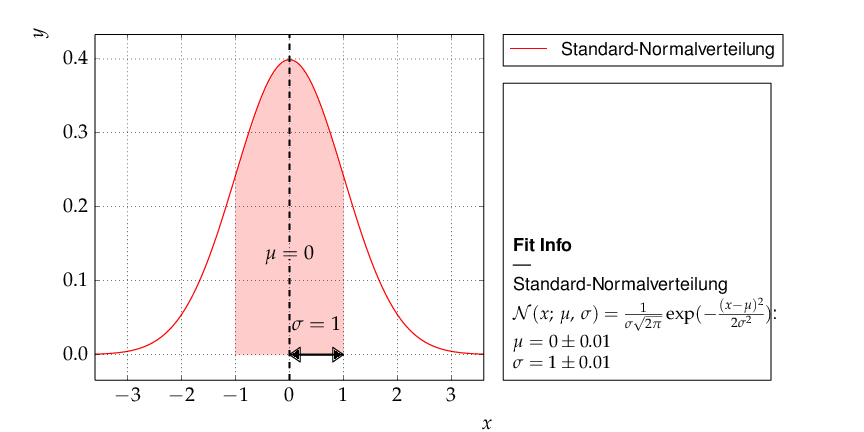
Here is the output, which shows that the parameters of the standard normal distribution, from which the data were generated, are reproduced well by the fit result:
Example 10 - plotting with kafe: properties of a Gauss curve¶
This example shows how to access the kafe plot objects
to annotate plots with matplotlib functionality.
A dummy object Dataset is
created with points lying exactly on a Gaussian curve.
The Fit will then converge toward
that very same Gaussian. When plotting, the data points
used to “support” the curve can be omitted.